[Backtracking] Combination Sum

Previous Posts:

[Backtracking] What is Backtracking? / Subsets

---

Problem: Combination Sum

The problem that we will solve in this post is the Combination Sum.

Combination Sum Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.

Understanding the Problem

First, let’s understand what the problem requires with a simple example.

If the input is [2,3,5] and the target is 8, we have to generate all the combinations of the input that sum up to the target.

We can also include the same number an unlimited number of times.

[2,2,2,2], [2,3,3], [3,5] will be the output of this example as they sum up to 7.

Solution

Visualization

To find the solution to this problem, we will try to visualize what should happen.

Becuase we want to identify every possible combinations to this problem, we can use backtracking.

The first naive approach is to create a recursive tree that looks like the diagram below.

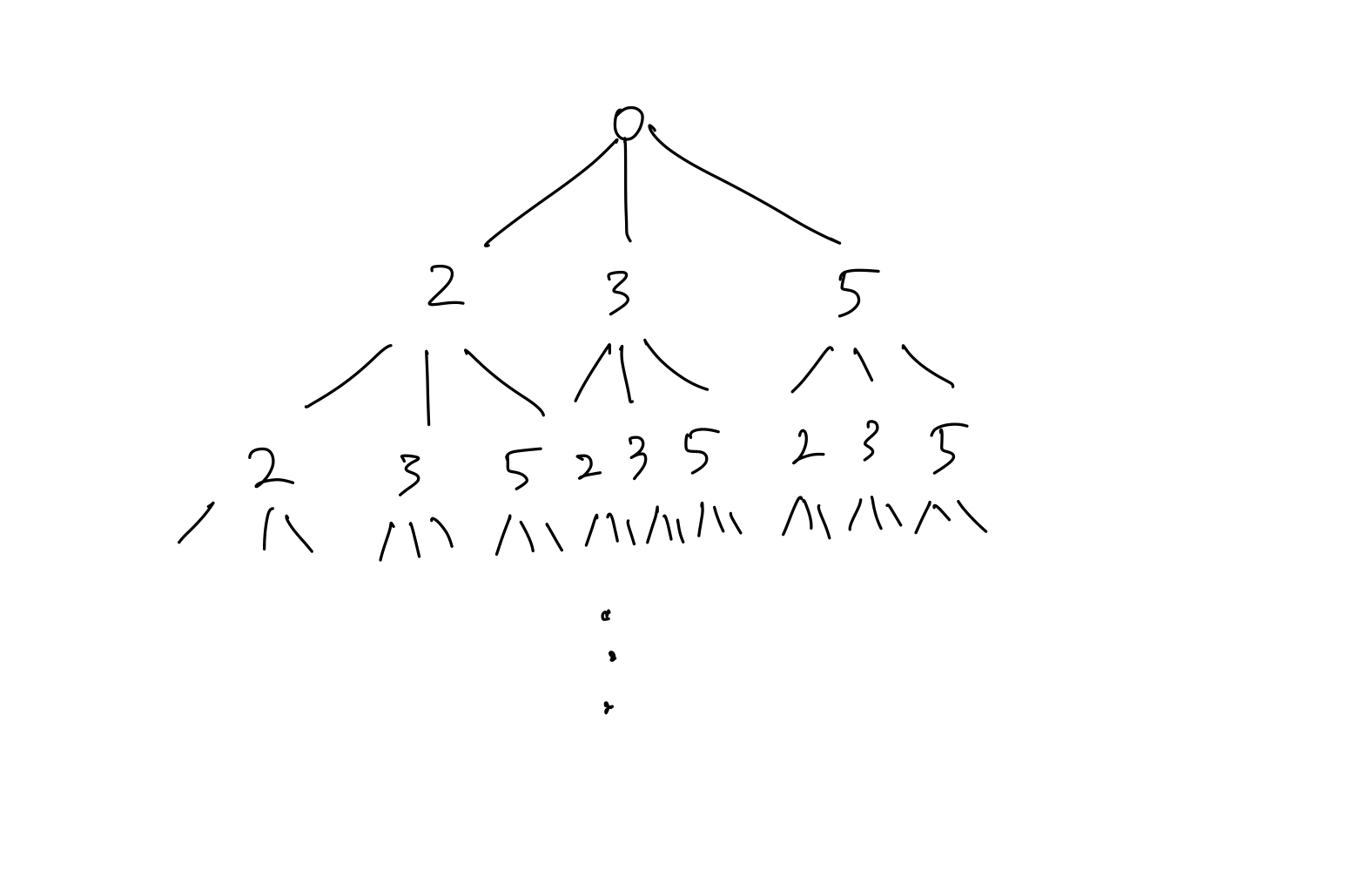
We can do a recursive tree traversal from the tree, add the combination when the sum equals to the target, and backtrack when the sum exceeds the target.

However, there is another constraint on this problem.

We have to return a list of all unique combinations.

If we follow the approach above, we will have non-unique combinations as two combinations are unique if the frequency of at least one of the chosen numbers is different.

For example, we can get both [2,3,3] and [3,3,2] from the traversal.

Therefore, we need another approach that will guarantee that all the combinations are unique.

To ensure this, we can traverse in a different way.

The key is to not include the previously searched element of the array as a candidate.

We will visualize the tree and see what this means.

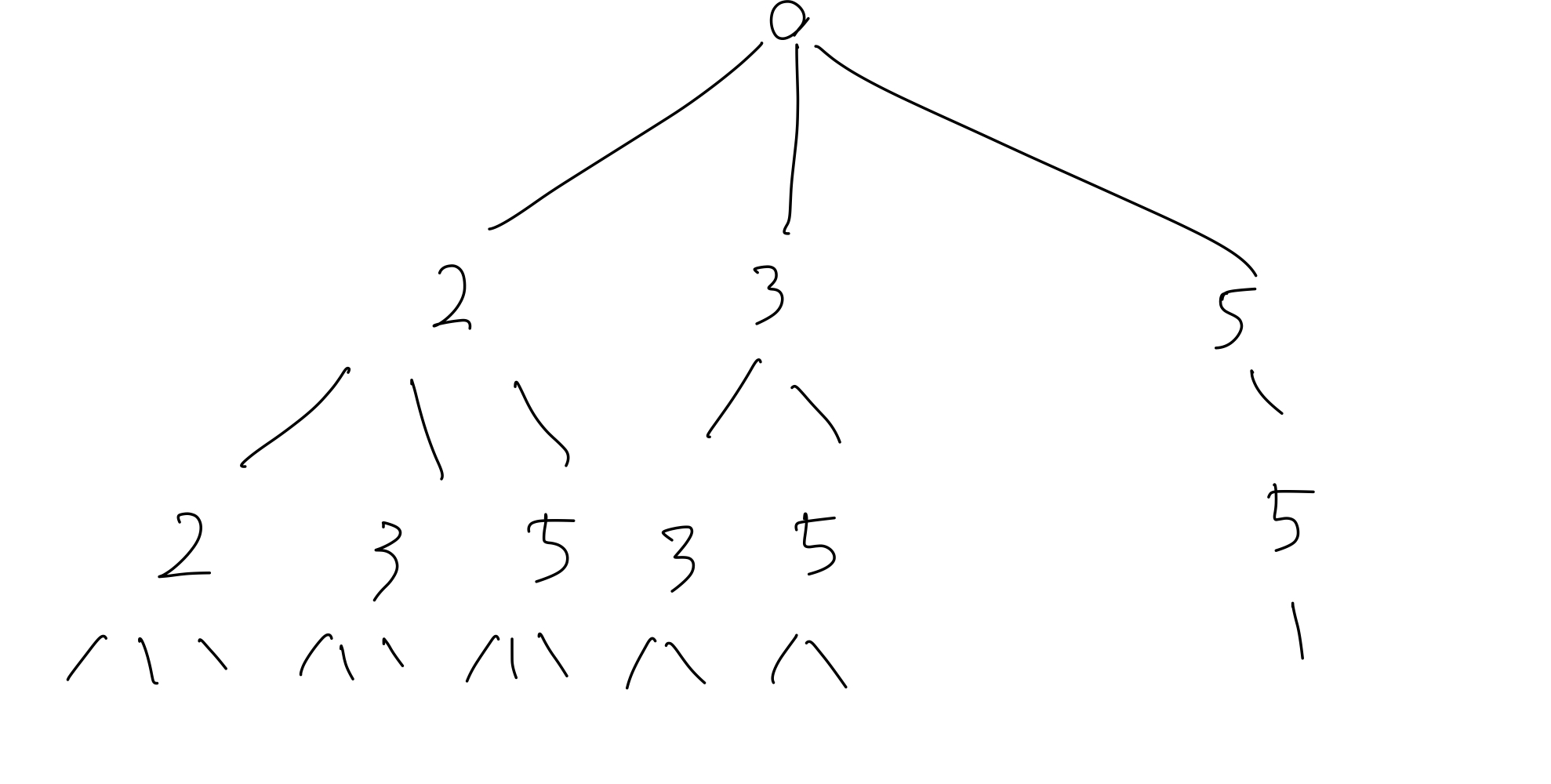
In this tree, the leftmost node from the root includes all the combinations that include 2. In the recursive search, it is guaranteed that all the combinations that include 2 will be added to our result.

For the middle node from the root, we start searching by including 3. At this point, we know that all the combinations that include 2 had been added to our output. Thus, we do not include 2 in this recursive search.

For the rightmost node from the root, we know that all the combinations that include 2 and 3 are added to our output. Thus, we do not include 2 or 3 in the recursive search.

By having this recursive structure, we can guarantee that all the combinations will be unique.

Code

Let’s look at the code that implements the recursive search from above.

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> combinations = new ArrayList<>();
        List<Integer> combination = new ArrayList<>();

        dfs(candidates, target, combinations, combination, 0, 0);

        return combinations;

    }

    // recursive depth-first search using backtracking
    public void dfs(int[] candidates, 
                    int target, 
                    List<List<Integer>> combinations, 
                    List<Integer> combination,
                    int sum,
                    int index){
        // base cases
        if(sum == target){
            // we add the copy of the combination because we are reusing it
            combinations.add(new ArrayList<>(combination));
            return;
        }else if(sum > target){
            // if sum exceed target, we return and backtrack
            return;
        }

        // for each child, we do recursive dfs
        for(int i = index; i < candidates.length; i++){
            // to do recursive dfs, add the element and update sum
            combination.add(candidates[i]);
            sum += candidates[i];

            // recursive dfs
            dfs(candidates, target, combinations, combination, sum, i);
            
            // now we are done with dfs on this node. backtrack.
            combination.remove(combination.size()-1);
            sum -= candidates[i];            
        }


    }
}

Reference https://leetcode.com/problems/combination-sum/