[Backtracking] What is Backtracking? / Subsets

Learning Backtracking

Backtracking is an algorithm that incrementally builds candidates to the solutions, and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot possibly be completed to a valid solution [1].

Usually, when we want to identify every possible solution to a problem, we can use backtracking to get the solutions.

Backtracking can be visualized in the form of a tree diagram, and it is the most intuitive way to understand the algorithm.

We will solve various computational problems to learn this algorithm.

Problem: Subsets

The problem that we will solve in this post is the subsets.

Subsets

Given an integer array nums of unique elements, return all possible subsets (the power set). The solution set must not contain duplicate subsets. Return the solution in any order.

This problem requires us to get all possible subsets of a given array.

Solution

Visualization

First, let’s think about the brute-force solution. The number of subsets is $2^n$, where n is the number of elements. This is because we can choose whether to include or not include each element.

Let’s start with a simple example nums = [1]. To get all the subsets, we can either choose to include 1 or not choose to include 1. This will give us the output is {[],[1]}. For another example nums = [1, 2], we have the same choice for 2 as well.

We can draw a tree diagram to visualize this problem with nums = [1, 2].

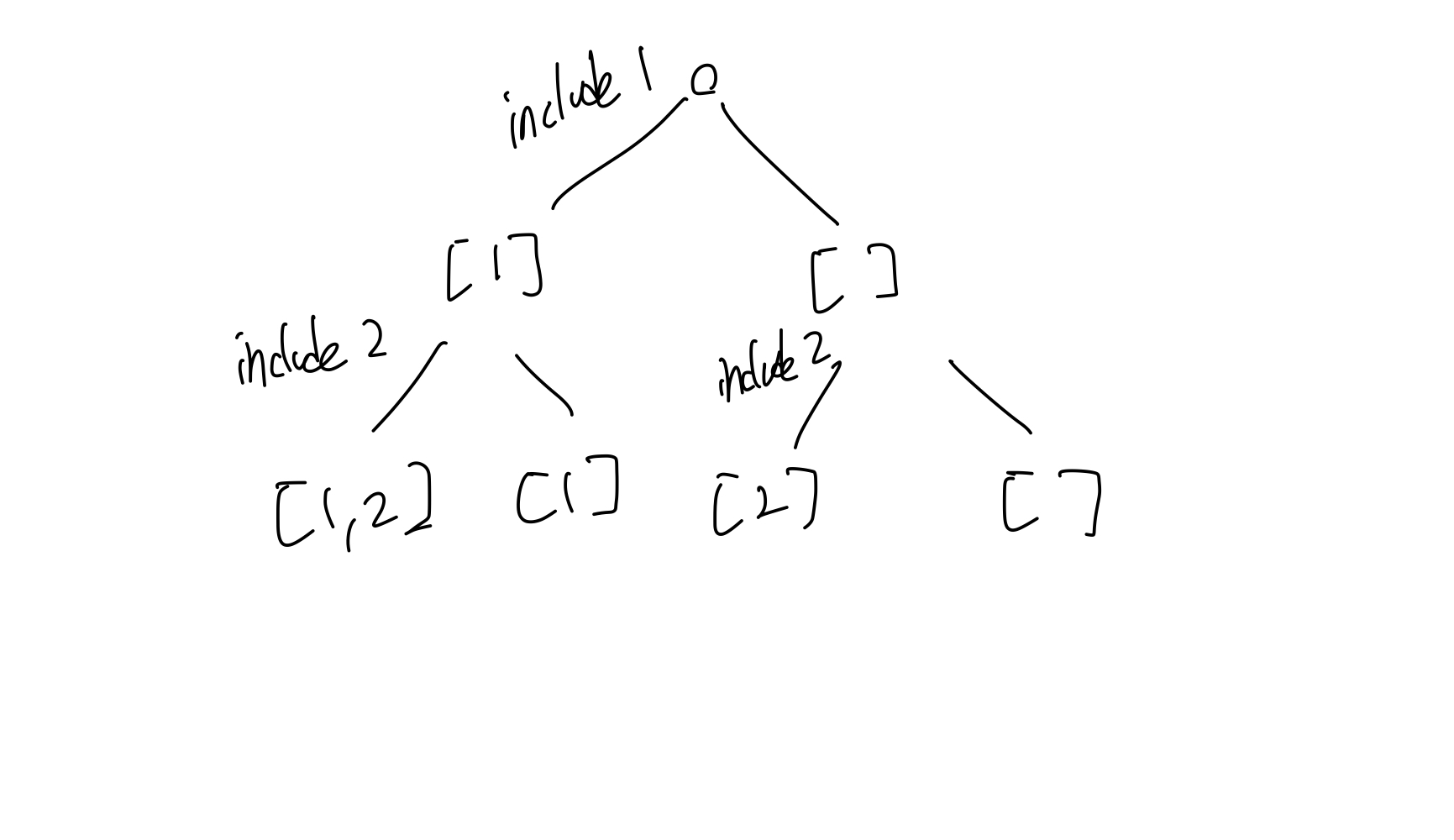
To get every possible subset, we can recursively depth-first traverse the tree and add the leaf nodes to the output. This recursive solution builds candidates to the solutions and backtracks (abandoning candidates) when there is no point in traversing more.

Code

Now let’s implement the solution that we visualized with the tree diagram.

class Solution {
    public List<List<Integer>> subsets(int[] nums) {

        List<List<Integer>> subsetsList = new ArrayList<>();
        List<Integer> subset = new ArrayList<>();

        dfs(nums, 0, subsetsList, subset);

        return subsetsList;
    }

    // use recursive dfs to traverse the tree 
    // and add all the leaf nodes
    public void dfs(int[] nums,  
                    int index, 
                    List<List<Integer>> subsetsList,
                    List<Integer> subset){

        // base case when we stop traversing
        if(index >= nums.length){
            // add the subset to our list
            // create a new instance because we are using subset again.
            subsetsList.add(new ArrayList<Integer>(subset));
            return;
        }
        
        // include element
        subset.add(nums[index]);
        // recursive dfs search (left node)
        dfs(nums, index+1, subsetsList, subset);

        // not inlcude element
        subset.remove(subset.size()-1);
        // recursive dfs search (right node)
        dfs(nums, index+1, subsetsList, subset);
    }
}

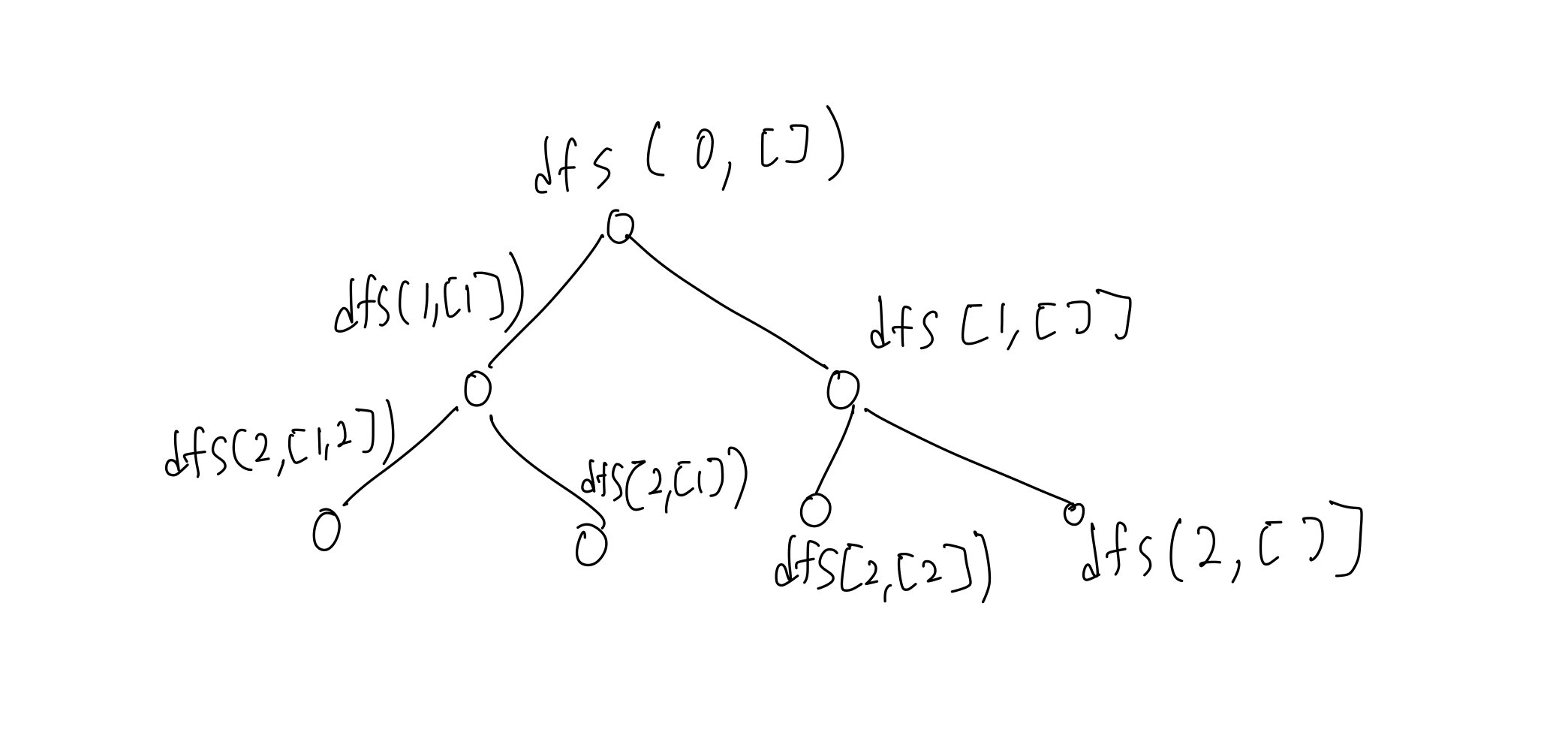
We can visualize the recursion tree for example nums = [1, 2].

Reference

[1] https://en.wikipedia.org/wiki/Backtracking

[2] https://leetcode.com/problems/subsets/